合作客戶/
拜耳公司 |
同濟大學 |
聯合大學 |
美國保潔 |
美國強生 |
瑞士羅氏 |
相關新聞Info
推薦新聞Info
-
> 強紫外線輻射對減縮劑抑制水泥石干縮變形效果研究(一)
> 無機粒子對TPAE界面張力、發泡、抗收縮行為的影響(四)
> 無機粒子對TPAE界面張力、發泡、抗收縮行為的影響(三)
> 無機粒子對TPAE界面張力、發泡、抗收縮行為的影響(二)
> 無機粒子對TPAE界面張力、發泡、抗收縮行為的影響(一)
> 弱堿三元采出液油水界面動態界面張力、強度、等特性研究
> 植保無人機噴頭和噴霧助劑對藥液表面張力、霧滴密度、覆蓋率的影響(二)
> 植保無人機噴頭和噴霧助劑對藥液表面張力、霧滴密度、覆蓋率的影響(一)
> 無人機噴霧作業下荔枝葉片上的表面張力、接觸角及霧滴沉積特性
> 不同界面張力-潤濕性組合的滲吸液體系對于化學滲吸效果的影響規律
光滑粒子流體動力學新方法及應用
來源:科學出版社 瀏覽 1114 次 發布時間:2022-10-31
近幾十年來,以計算流體力學為基礎的數值模擬技術取得了巨大成功,成為繼理論研究和實驗研究兩種傳統方法之外的第三種關鍵手段。針對國防工程領域中極端復雜的流動問題,一些原來認為難以解決的問題,在數值模擬技術的幫助下都能夠迎刃而解。無網格數值方法由于可以從本質上解決網格法在求解大變形和自由表面流動過程時遇到的網格扭曲、纏繞或者界面追蹤的技術難題,已迅速成為計算力學方法研究的一個熱點。光滑粒子流體動力學(SPH)便是這類方法中發展最為迅速、應用最為廣泛的一種方法。
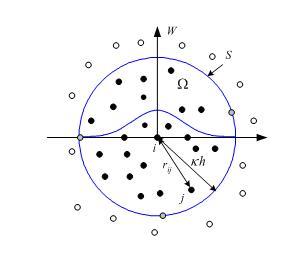
SPH光滑核函數
SPH可應用于的典型領域
光滑粒子流體動力學是20世紀70年代提出并逐漸發展起來的一門數值計算方法,由于具有自適應性、無網格性、拉格朗日性以及粒子性等特性,其在求解大變形、自由表面流、復雜界面運動等過程中具有較大優勢,已廣泛應用于天體物理、沖擊爆炸、水動力學等領域。伴隨著高性能計算機以及虛擬現實、互聯網、云計算等新興技術的快速發展,以SPH為代表的新一代數值模擬方法必將迎來新的發展機遇。同時,發展以新的數值仿真技術為核心的計算機輔助工程必將為提升我國的工業信息化水平發揮重要作用。
《光滑粒子流體動力學新方法及應用》闡述了作者及其研究團隊近20年來在SPH方法及應用方面取得的最新研究成果,這些研究成果不僅涵蓋SPH方法研究的主要領域,而且集中對SPH方法前沿問題和尖端問題進行探討,詳細論述對這些問題的解決方案,同時引入新的理論,開拓新的應用領域,不僅有助于讀者快速解決在SPH研究方面存在的難題,指導相關領域內的研究工作,而且有助于加快讀者在該方法方面的創新,取得更大的理論突破。
全書從方法和應用兩個層面上闡述最新的研究成果:
方法層面新在哪些方面?
完全變光滑長度SPH方法
從對稱核近似出發,建立一組非常適合于模擬爆炸與沖擊、大變形大扭曲等密度和光滑長度變化劇烈問題的修正變光滑長度SPH方程組,修正SPH密度演化方程、動量方程以及能量方程與變光滑長度方程的關聯效應,從根本上來消除變光滑長度效應在求解極端爆炸問題時造成的偏差。
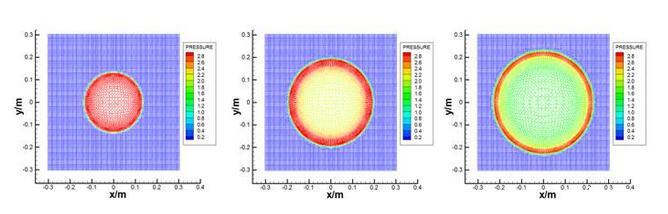
二維Sedov問題的完全變光滑長度SPH方法計算結果
無網格局部間斷伽遼金方法
從理論上融合先進的無網格離散技術和成熟高效的網格CFD求解技術,首先從擴展網格間斷伽遼金方法的空間離散技術入手,建立出更具幾何靈活性和實用性的無網格CFD方法——無網格局部間斷伽遼金(MLDG)法及其衍生算法,同時從該方法出發,重新構建SPH方法的本理論,建立一類特殊的拉格朗日型MLDG法——間斷伽遼金型SPH方法,并從數值流通量的概念來考察傳統SPH方法以及基于Riemann解的SPH方法,從而能夠理論上統一網格方法中數值流通量技術在SPH方法中的運用。然后,在此基礎上引入網格方法通量校正(FCT)技術,建立更為完善的不依賴人工黏性的Godunov-SPH-FCT格式,從而提高SPH在求解激波問題方面的能力。
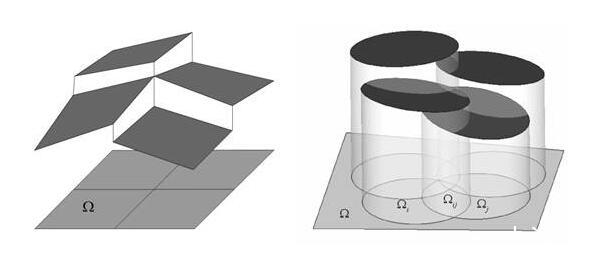
網格間斷伽遼金方法(左)和無網格間斷伽遼金方法(右)
SPH拉伸不穩定問題研究
在Swegle等對SPH進行von Neumann穩定性分析的基礎上,根據von Neumann穩定性分析方法的思想,論述速度小擾動穩定性測試法,分別研究不同核函數、不同動量方程離散形式和不同擾動波長下SPH的穩定性,同時對應力點法、拉格朗日核函數法、守恒光滑法、人工應力法以及修正的光滑粒子法對SPH的穩定效果進行穩定分析,研究每種方法解決或改善SPH的拉伸不穩定性情況,并加以比較分析,尋找有效實用的人工應力法作為改善SPH拉伸不穩定性問題的方法。
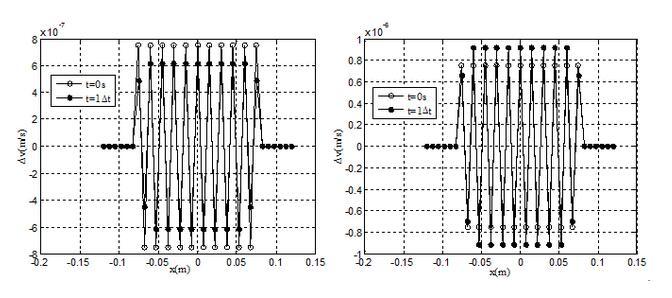
壓縮狀態下速度擾動振幅變化(左)和拉伸狀態下速度擾動振幅變化(右)
三次B-樣條核函數穩定性分析
SPH-FEM耦合算法
為解決計算力學中的大變形問題,建立一系列SPH-FEM耦合算法:①固結;②接觸;③轉換。其中,SPH-FEM固結算法適用于同一物體內部,如沖擊問題中將靶板的彈著點區域離散為SPH粒子,其余部分離散為有限單元;SPH-FEM接觸算法適用于不同物體之間,如流固耦合問題中將流體離散為SPH粒子,固體離散為有限單元;SPH-FEM轉換算法適用于大變形位置和范圍未知的情況,如裂紋擴展問題,問題域初始離散為有限單元,計算中裂紋擴展方向上的有限單元轉換為SPH粒子。
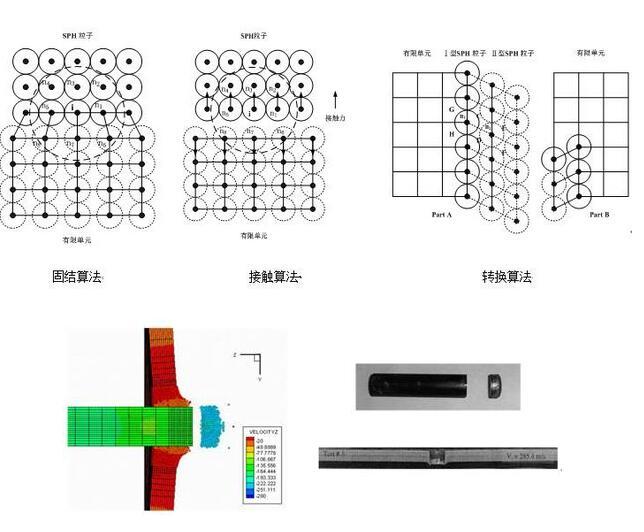
平頭鋼彈正沖擊鋼板SPH-FEM耦合方法計算結果(左)和實驗結果[50](右)對比
SDPH-FVM耦合算法
為解決現有模型和算法在求解氣-粒兩相流動問題遇到的不足,基于顆粒動力學模型,通過增加SPH粒子所表征的顆粒的材料屬性,推導SPH粒子屬性與顆粒屬性間的關系式,將SPH改造成適于離散相求解的SDPH方法,建立SPH粒子與真實顆粒間的一一對應關系;在此基礎上,分別采用SDPH方法和FVM對TFM模型中的離散相和連續相進行求解,推導SDPH和FVM離散方程組,搭建SDPH與FVM耦合框架,實現SDPH-FVM耦合算法流程。
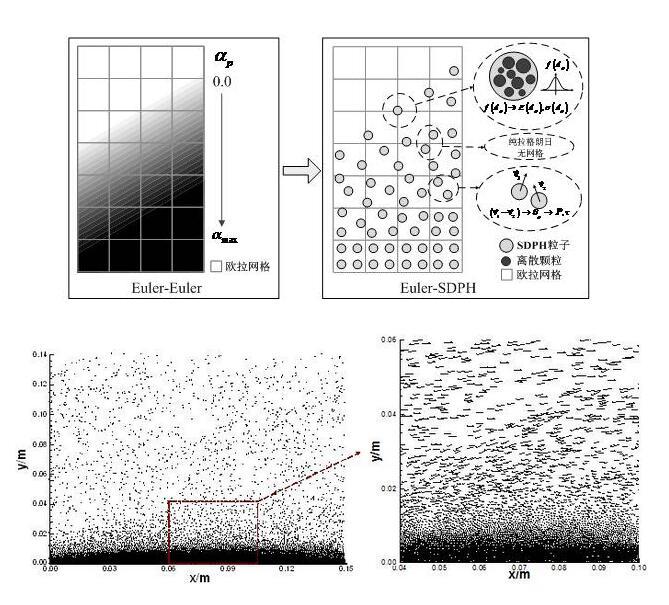
風沙運動穩定后粒子空間分布(左)和速度空間分布(右)
基于CSF模型的表面張力修正算法
從CSF模型出發,在Morris提出的表面張力SPH方法基礎上,采用能夠很好解決邊界核插值問題的CSPM方法對表面張力算法進行修正,得到修正后的表面張力方程組;在此基礎上,采用新的邊界處理方式和法向修正方法對傳統方法進行改進,同時引入Brackbill提出的壁面附著力邊界條件處理方法,得到含壁面附著力邊界條件的SPH表面張力算法,解決現有表面張力算法在求解液滴等微流體變形運動時存在的不足。
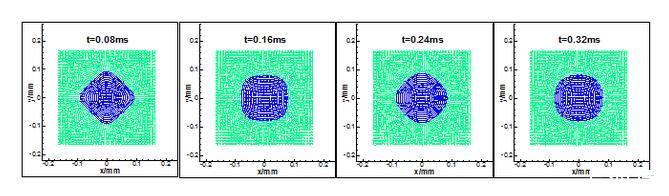
初始方形液滴在表面張力作用下變化過程
SPH方法固壁邊界模型
對SPH方法中的邊界施加方法進行探討,分析目前常用的邊界施加方法——罰方法及虛粒子法的施加原理,分別在這兩種方法基礎上進行相應地改進,并設計了部分算例對固壁邊界施加方法的有效性進行驗證。
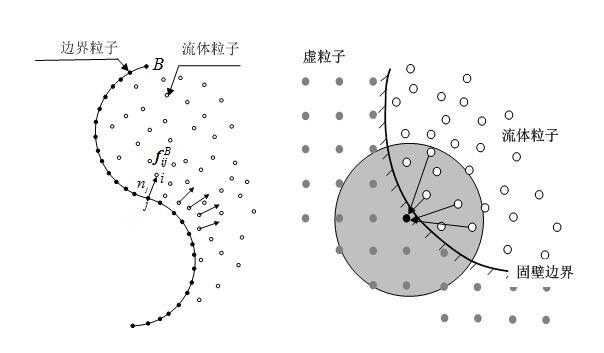
罰函數方法示意圖(左)和虛粒子方法示意圖(右)
應用層面新在哪些方面?
SPH方法應用于爆炸領域
爆炸問題在國民經濟和科學技術中有著廣泛而重要的應用。在國防領域,為了進行各種武器的研制開發,需要全面研究爆炸、侵徹的基本規律和作用原理。爆炸所產生的沖擊波和碎片的毀傷效應是衡量武器效果的重要標志,只有對其規律進行深入研究,才能有效指導戰斗部的設計以及裝備的安全防護。在民用領域,利用工程爆破進行隧道開挖、采礦作業,需要對炸藥的選擇使用、對巖土的動態響應以及破壞方式等爆破效果進行準確評估。另外,隨著爆炸焊接、爆炸切割等爆炸加工技術在工程上的廣泛應用,利用爆炸的能量驅動金屬板、利用爆炸沖擊壓實材料和利用爆炸沖擊合成生成金剛粉末等越來越普遍,對爆炸相關問題的研究要求逐漸提高。本書采用考慮變光滑長度和多相界面的SPH方法對爆炸問題進行模擬,解決了爆炸中密度和光滑長度變化劇烈以及不同材料界面處密度相差很大但壓強連續的問題,模擬了錐孔炸藥爆炸、聚能射流形成以及中心球起爆等過程,對物理現象進行了分析。
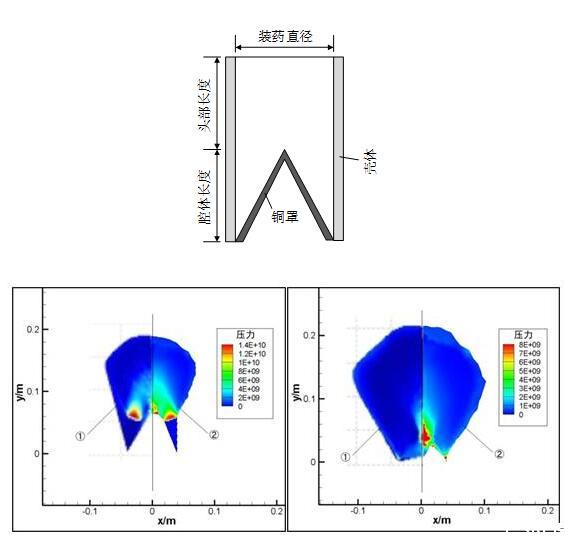
①和②分別表示傳統方法和完全變光滑長度SPH方法模擬的結果
炸藥在爆轟過程中的壓強分布對比
SPH方法應用于沖擊動力學領域
沖擊動力學是研究結構和材料在沖擊載荷作用下的運動、變形和破壞規律的學科。經過近100年的發展,沖擊動力學問題已經在航空航天、防災減災、材料科學、工程結構設計、終點效應學、巖土工程、武器效能評估等眾多領域得到了廣泛應用,既有重要的理論學術價值,又有廣闊的工程和軍事應用需求。本書論述SPH方法在具有材料強度的沖擊動力學中的應用,將具有材料強度的物質的本構模型和狀態方程引入SPH方程中,用以模擬分析在高速沖擊和穿透的情況下具有材料強度的流體動力學問題,如30CrMnSiA鋼板抗槍彈沖擊的SPH-FEM模擬及聚能射流侵徹混凝土過程。
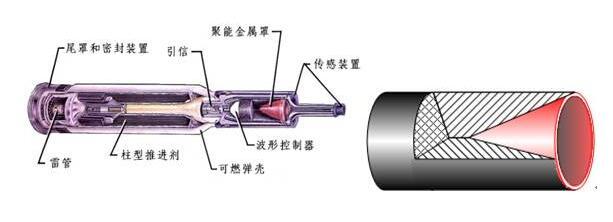
聚能射流裝置示意圖
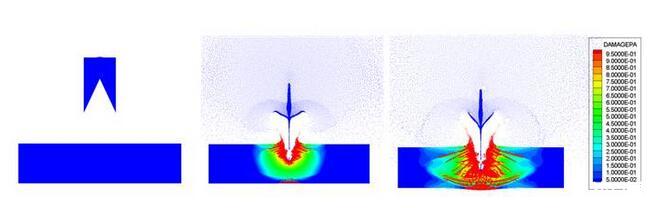
聚能射流侵徹混凝土靶板過程

沖擊多層樓板計算結果
SPH應用于水動力學領域
水動力學作為研究水和其他液體運動規律及其與邊界相互作用的學科,在航空、航天、航海、水能、采油和醫學等領域中應用較為廣泛,不僅涉及理想流體運動、黏性流體運動,還包括自由表面流、多相流、非牛頓流以及空化流等多種流動形式。本書在多相黏流SPH方法的基礎上,結合新的邊界力計算方法,進行了包括二維潰壩、液體攪拌、物塊落水及小球撞擊水面等問題的數值模擬。
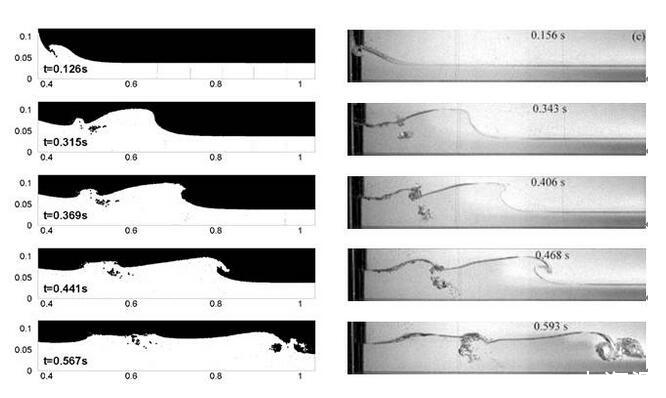
潰壩仿真結果(左)和實驗結果[19](右)對比
SPH應用于流體碰撞霧化領域
液體火箭發動機中,推進劑的霧化特性對燃燒穩定性和推力特性有著巨大影響,推進劑的霧化可分為一次霧化和二次霧化兩個過程,一次霧化主要發生在噴注面附近,是指由噴注器噴射出來的推進劑射流相互碰撞形成液膜,然后液膜破碎形成不穩定的液絲,進而斷裂、收縮成為液滴的過程;二次霧化是指一次霧化形成的液滴進一步碰撞破碎的過程。,開展推進劑一次霧化與二次霧化研究對于改進推進劑配方設計,提高發動機性能具有重要作用。除液體火箭發動機內的噴注霧化,流體的碰撞霧化及流體液滴的聚合破碎等現象在工業和自然界中廣泛存在,例如,汽車工業中內燃機內的燃料霧化,化學工業中的乳化、萃取,環保工業中的廢物處理,自然界中雨雪的形成等,因此它們的預測和控制至關重要。本書應用SPH方法對液滴碰撞、液滴在流場中的二次破碎、液滴在氣固交界面的變形移動等典型過程進行了數值模擬,在此基礎上,進一步模擬了更為復雜的凝膠推進劑霧化過程。
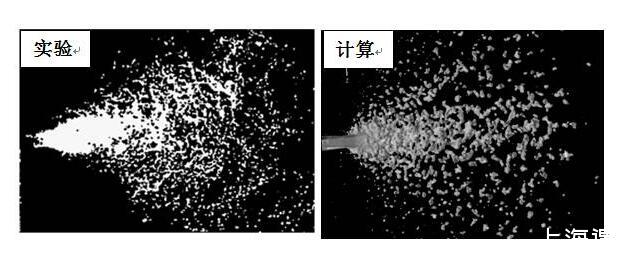
兩股牛頓流體射流互擊過程實驗結果[5]和計算結果對比

異種難溶液滴碰撞過程中實驗形態[2]和計算形態對比
SPH應用于鑄造充型領域
金屬液充型過程是復雜的高溫、瞬時的流動過程,飛濺、氧化等物理和化學變化使鑄件內部容易產生缺陷。直接觀察金屬液的充型狀態難度較大,數值模擬技術對預測諸多鑄造缺陷,如氣孔、夾渣、冷隔、澆不足等起到關鍵性作用,是優化模具設計、保證鑄件質量、改進工藝過程、降低生產成本的有效手段。為充型過程研究提供了一種高效、廉價的方法,對研究金屬充型具有不可替代的作用。本書采用新型罰方法邊界力模型,對球形模具和弓形模具填充過程進行了數值模擬研究。

S形型腔充型過程的SPH數值模擬結果和實驗結果[9]對比
本文摘編自強洪夫著《光滑粒子流體動力學新方法及應用》一書文前部分,內容有刪節。
強洪夫著
光滑粒子流體動力學新方法及應用
光滑粒子流體動力學(SPH )方法是近年來興起并逐漸得到廣泛應用的一種數值模擬方法,對該方法進行研究具有很大的科學價值和實際意義。本書是論述SPH 新方法及應用方面的一本專著,匯集了作者及其研究團隊近20年來的研究成果和研究經驗,系統闡述SPH 方法基礎理論、完全變光滑長度SPH 方法、無網格局部間斷伽遼金方法、SPH 拉伸不穩定問題、SPH -FEM耦合算法、SDPH-FVM耦合算法、基于csf模型的表面張力算法以及SPH 方法固壁邊界模型等一系列新方法、新模型的思想和實現途徑,開拓了SPH 方法在爆炸模擬、沖擊動力學、水動力學、流體碰撞霧化問題以及鑄造充型等新領域中的應用。本書敘述力求簡明扼要,重點突出。










